Jugando con los Númer0s Enter0s
Números enteros
Recuerdan cuando eran niños y aprendían a diferenciar los números, si estos eran reales, enteros, irracionales, etc. Pues hoy recordaremos todo ello, como se operan y como estas operaciones nos ayudan en la vida diaria.
Números enteros
Un
número entero es cualquier elemento del conjunto formado
por los números naturales,
sus opuestos (versiones
negativas de los naturales) y el cero.
Estos son:
Suma de números enteros
1. Si los números
enteros tienen el mismo signo, se suman los valores absolutos y al resultado se
le coloca el signo común.
3 + 5 = 8
(−3) + (−5) = − 8
2. Si números enteros
son de distinto signo, se restan los valores absolutos (al mayor le restamos el
menor) y al resultado se le coloca el signo del número de mayor valor absoluto.
− 3 + 5 = 2
3 + (−5) = − 2
Propiedades de la suma de números
enteros
1. Interna:
·
a + b Pertenece enteros
3 + (−5) Pertenece enteros
2. Asociativa:
·
(a + b) + c = a + (b + c) ·
(2 + 3) + (− 5) = 2 + [3 + (− 5)]
5 − 5 = 2 + (− 2)
0 = 0
3. Conmutativa:
·
a + b = b + a
2 + (− 5) = (− 5) + 2
− 3 = − 3
4. Elemento neutro:
·
a + 0 = a
(−5) + 0 = − 5
5. Elemento opuesto
·
a + (-a) = 0
5 + (−5) = 0
−(−5) = 5
Resta de números
enteros
La diferencia de
los números enteros se obtiene sumando al minuendo el
opuesto del sustraendo.
a
- b = a + (-b)
7
− 5 = 2
7
− (−5) = 7 + 5 = 12
Propiedades de la resta de
números enteros
1. Interna:
a
− b 

10 − (−5) 

2. No es
Conmutativa:
a
- b ≠ b - a
5 − 2 ≠ 2 − 5
Multiplicación
de números enteros
La multiplicación de
varios números enteros es otro número entero, que
tiene como valor absoluto el producto de los valores absolutos y,
como signo, el que se obtiene de la aplicación de la regla
de los signos.
Regla de los
signos

2 · 5 = 10
(−2) · (−5) = 10
2 · (−5) = − 10
(−2) · 5 = − 10
Propiedades de
la multiplicación de números enteros
1. Interna:
a
· b 

2 · (−5) 

2. Asociativa:
(a
· b) · c = a · (b · c)
(2 · 3) · (−5) =
2· [(3 · (−5)]
6 · (−5) = 2 · (−15)
-30 = -30
3. Conmutativa:
a · b = b · a
2 · (−5) = (−5) ·
2
-10 = -10
4. Elemento neutro:
a ·1 = a
(−5)· 1 = (−5)
5. Distributiva:
a · (b + c) = a · b + a · c
(−2)· (3 + 5) =
(−2) · 3 + (−2) · 5
(−2)· 8 =- 6 - 10
-16 = -16
6. Sacar factor
común:
a
· b + a · c = a · (b + c)
(−2) · 3 + (−2) ·
5 = (−2) · (3 + 5)
División de números
enteros
La división de dos
números enteros es otro número entero, que tiene
como valor
absoluto el cociente de los valores absolutos y, como signo,
el que se obtiene de la aplicación de la regla de los signos.
10 : 5 = 2
(−10) : (−5) = 2
10 : (−5) = − 2
(−10) : 5 = − 2
Propiedades de
la división de números enteros
1. No es una
operación interna:
(−2)
: 6 
2. No es
Conmutativo:
a
: b ≠ b : a
6 : (−2) ≠ (−2) : 6
Jugando con los Númer0s Enter0s
 Reviewed by Andrea Ramos
on
noviembre 20, 2019
Rating:
Reviewed by Andrea Ramos
on
noviembre 20, 2019
Rating:
 Reviewed by Andrea Ramos
on
noviembre 20, 2019
Rating:
Reviewed by Andrea Ramos
on
noviembre 20, 2019
Rating:


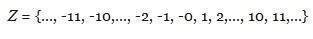














No hay comentarios: