Identidad de Legendre

Productos notables

Hola, hoy aprenderemos mas acerca de los productos notables, como podemos memorizar dichas formulas dependiendo a que producto sea, como gratificarlo y usarlo como dinámica. Mil y un formas de aprender dicho tema ¿Te unes?


Se llama productos notables a ciertas expresiones algebraicas que se encuentran frecuentemente y que es preciso saber factorizarlas a simple vista; es decir, sin necesidad de hacerlo paso por paso.

Se les llama productos notables (también productos especiales) precisamente porque son muy utilizados en los ejercicios.

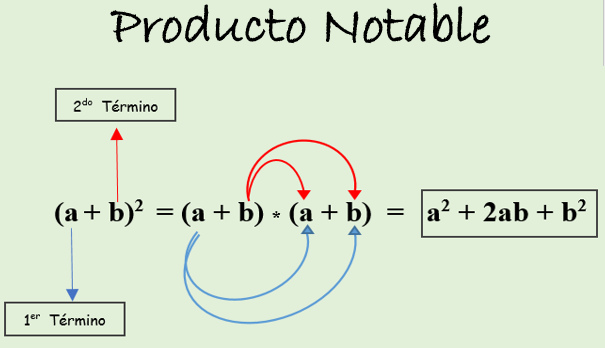
Binomio al cuadrado

Es la multiplicación de un binomio por sí mismo, expresada en forma de potencia, donde los términos son sumados o restados:

a. Binomio de suma al cuadrado: es igual al cuadrado del primer término, más el doble del producto de los términos, más el cuadrado del segundo término. Se expresa de la siguiente manera:

(a + b)2 = (a + b) * (a + b).

b. Binomio de una resta al cuadrado: se aplica la misma regla del binomio de una suma, solo que en este caso el segundo término es negativo. Su fórmula es la siguiente:

(a – b)² = [(a) + (- b)]²

(a – b)² = a² +2a _* (-b) + (-b)²

(a – b)²   = a² – 2ab + b².

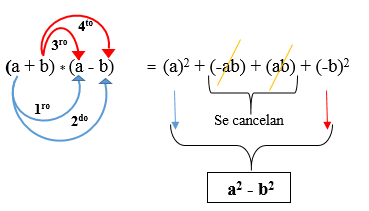
Diferencia de cuadrados

Dos binomios son conjugados cuando los segundos términos de cada uno son de signos diferentes, es decir, el del primero es positivo y el del segundo negativo o viceversa. Se resuelve elevando cada monomio al cuadrado y se restan. Su fórmula es la siguiente:

(a + b) * (a – b)

En la siguiente figura se desarrolla el producto de dos binomios conjugados, donde se observa que el resultado es una diferencia de cuadrados.

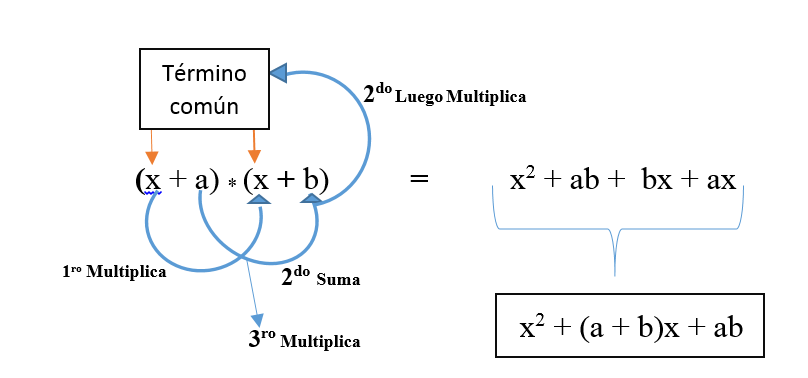
Producto de dos binomios con un término común

Es uno de los productos notables más complejos y poco utilizados porque se trata de una multiplicación de dos binomios que tienen un término en común. La regla indica lo siguiente:

·         El cuadrado del término común.

·         Más la suma los términos que no son comunes y luego multiplicarlos por el término común.

·         Más la suma de la multiplicación de los términos que no son comunes.

Se representa en la fórmula: (x + a) * (x + b)

Binomio al cubo

Es un producto notable complejo. Para desarrollarlo se multiplica el binomio por su cuadrado, de la siguiente manera:

a. Para el binomio al cubo de una suma:

·         El cubo del primer término, más el triple del cuadrado del primer término por el segundo.

·         Más el triple del primer término, por el segundo al cuadrado.

·         Más el cubo del segundo término.

(a + b)3 = (a + b) * (a + b)2

(a + b)3 = (a + b) * (a2 + 2ab + b2)

(a + b)3 = a3 + 2a2b + ab2 + ba2 + 2ab2 + b3

(a + b)3 = a3 + 3a2b + 3ab2 + b3.

b. Para el binomio al cubo de una resta:

·         El cubo del primer término, menos el triple del cuadrado del primer término por el segundo.

·         Más el triple del primer término, por el segundo al cuadrado.

·         Menos el cubo del segundo término.

 (a – b)3 = (a – b) * (a – b)2

(a – b)3 = (a – b) * (a2 – 2ab + b2)

(a – b)3 = a3 – 2a2b + ab2 – ba2 + 2ab2 – b3

(a – b)3 = a3 – 3a2b + 3ab2 – b3.

 

Identidad de Legendre

Se aplica la identidad de LEGENDRE cuando los binomios tienen la siguiente forma y te conviene memorizar: